How to Find Out HCF (Highest Common Factor) and LCM (Least Common Multiple)? Learn Tricks and Strategies to Solve The Problems Clearing Doubts Conceptually!

Abstract:

HCF (Highest Common Factor) and LCM (Least Common Multiple) concepts are the foundation of many mathematical operations and are essential in solving complex problems. HCF and LCM problems challenge your ability to find the greatest common factor and the smallest common multiple of numbers, and they require both logical and mathematical skills. 

Keywords: HCF (Highest Common Factor), LCM (Least Common Multiple)

Learning Outcomes:

We delve into the world of HCF and LCM problems and explore the exciting ways they can be used to solve challenging aptitude questions!

Introduction 

What is HCF (Highest Common Factor)?

The Highest Common Factor (HCF) of two numbers is the highest possible number that divides both numbers completely. The Highest Common Factor (HCF) is also known as the Greatest Common Divisor (GCD). Or Greatest Common Factor (GCF). Among all three terms HCF is more frequently used.

How to Find out HCF?

There are 3 methods to calculate the HCF of two numbers:

1. HCF by listing factors method

2. HCF by prime factorization

3. HCF by division method

1. HCF by Listing Factors Method

Step 1: Here, we list the factors of each number and find the common factors of those numbers. 

Step 2: Then, among the common factors, we determine the highest common factor. 

Example 1:

Example 2: Find the HCF of 32 and 14.

Solution 

Step 1: List down the factors 

Here, the factors of 32 and 14 are 

- The factors of 32 are: 1, 2, 4, 8, 16, 32

- The factors of 14 are: 1, 2, 7, 14

Step2:  Examine common Factors 

We can see that 1, 2 are the only common factors of 32 and 14. 

Step 3: Find out the greatest common factor

Here 2 is the greatest among all the common factors.

Hence, HCF of 32 and 14 is 2.

2. HCF by Prime Factorization

We can find HCF using Prime factorization method of the given numbers. 

Follow the steps below to calculate the HCF of given numbers using the prime factorization method:

First, Find the common prime factors of the given numbers.

Multiply these common prime factors to obtain the HCF of those numbers.

Example:

Find the HCF of 80 and 90.

Solution:

The prime factors of 80: 2 * 2 * 2 * 2 * 5; 

The prime factors of 90: 2 * 3 * 3 * 5.

We can see that 2, 5 are the only common factors of 80 and 90, Now, the HCF of 80 and 90 will be the product of the common prime factors, which are 2 and 5. 

Hence, HCF of 80 and 90 is 10.

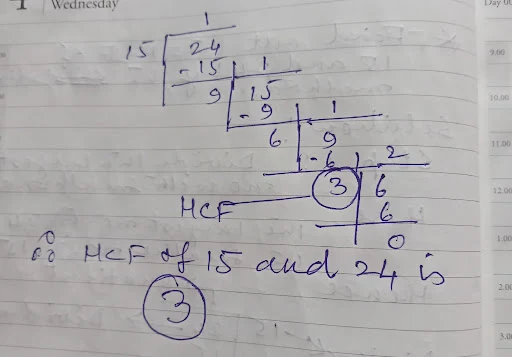
3. HCF by Division Method

The HCF of two numbers can be calculated using the division method. 

Follow the steps below to calculate the HCF of given numbers using the Division Method

Step 1: First, we divide the larger number by the smaller number and check the remainder.

Step 2: Then, make the remainder of the previous step as the new divisor and the divisor of the previous step becomes the new dividend. 

Step 3: After this we perform the long division again.

Step 4: Continue the long division process till we get the remainder as 0. 

It should be noted that the last divisor will be the HCF of those two numbers.

Example:

Find the HCF of 30 and 42.

Solution

HCF of 30 and 42

Hence, HCF of 30 and 42 is 6.

What is LCM (Least Common Multiple)?

In arithmetic, the LCM or least common multiple of two numbers a and b, is denoted as LCM (a,b) is the smallest or least positive integer that is divisible by both a and b. 

LCM is also called the Least Common Divisor

Example:

Let’s take two positive integers 3 and 4, the task is to find the LCM(3, 4).

Solution:

Multiples of 3: 3,6,9,12,15,18,21,24…

Multiples of 4: 4,8,12,16,20,24, 28…

The common multipliers of 3 and 4 are 12, 24…, So, the least common multiple is 12.

Hence, LCM(3, 4) = 12

How to Find LCM?

There are 3 methods to find the least common multiple of two numbers.

1. LCM by Listing Method

2. LCM by Prime Factorization Method

3. LCM using Division Method

1. LCM by Listing Method:

LCM by Listing Method

We can find out the common multiples of two or more numbers by listing their multiples. Out of these common multiples, the least common multiple is considered and the LCM of two given numbers can thus be calculated. To calculate the LCM of the two numbers A and B by the listing method, we use the steps given below:

• Step 1: List the first few multiples of A and B.
• Step 2: Mark the common multiples from the multiples of both numbers.
• Step 3: Select the smallest common multiple. That lowest common multiple is the LCM of the two numbers.

Example:

Find LCM of two positive integers 2 and 6.

Solution:

Multiples of 2: 2,4,6,8,10,12,14…

Multiples of 6: 6,12,18,24, 30…

The common multipliers of 2 and 6 are 6, 12…, So, the least common multiple is 6.

Hence, LCM(2, 6) = 6

2. LCM by Division Method:

In order to find the LCM by division method, we divide the numbers by a common prime number, and these prime factors are used to calculate the LCM of those numbers. Let us understand this method using the steps given below:

• Step 1: Find a prime number which is a factor of at least one of the given numbers. Write this prime number on the left of the given numbers.
• Step 2: If the prime number in step 1 is a factor of the number, then divide the number by the prime and write the quotient below it. If the prime number in step 1 is not a factor of the number, then write the number in the row below as it is. Continue the steps until 1 is left in the last row.

Example:

Let’s take two positive integers 3 and 4, the task is to find the LCM(3, 4).

Solution:

LCM(3,4) = 12

The LCM is the product of all these prime numbers.

Hence, LCM(3, 4) = 12

3. LCM by Prime Factorization Method:

By using the prime factorization method we can find out the LCM of the given numbers. To calculate the LCM of two numbers using the prime factorization method, we use the steps given below:

• Step 1: Find the prime factors of the given numbers by repeated division method.
• Step 2: Write the numbers in their exponent form. Find the product of only those prime factors that have the highest power.
• Step 3: The product of these factors with the highest powers is the LCM of the given numbers.

Example:

Find out the LCM of 32, 48 and 72

Solution:

Hence, 

LCM of 

32, 48 and 72 = 

2 × 2 × 2 × 2 × 2 × 3 × 3 

= 288

How to Find HCF and LCM of a Fraction?

HCF of a fraction: 

HCF of Numerators / LCM of Denominators.                           

LCM of a fraction: 

LCM of Numerators / HCF of Denominators.

Example                                                      

Q. Find the HCF and LCM of 1/3 , 8/7, 9/11.

Solution:

LCM of given numbers : LCM(1,8,9)/ HCF (3,7,11) = 72/1.

HCF of given numbers : HCF(1,8,9) / LCM(3,7,11) 

= 1/231.

Conclusions :

The complete form of HCF is highest common factor, and that of LCM is the lowest common factor.

 

The HCF of two or more numbers is the greatest number that divides each of them fully. 

The LCM of those numbers is the least number that can be exactly divisible by two or more given numbers.

The greatest common factor (HCF) is also known as the greatest common factor (HCF), while the least common multiple (LCM) is also known as the least common multiple (LCM). 

In any pair of numbers, the product of the HCF and LCM is always equal to the product of those two numbers, and the reverse is true as well.