Chapter 5: Fuzzy Measures and Integrals
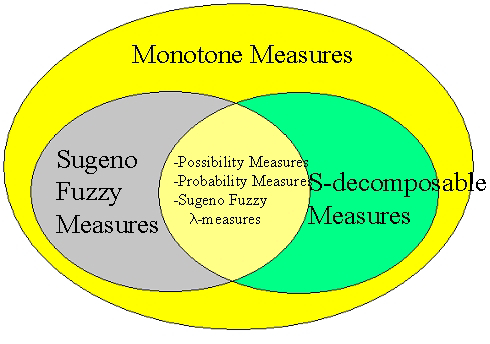
5.1 Introduction In classical mathematics, measures are functions that assign a real number to a set, typically representing size, probability, or weight. In fuzzy set theory, where uncertainty and vagueness prevail, fuzzy measures and fuzzy integrals extend these ideas to model imprecise information. These concepts are crucial in applications such as decision-making, information aggregation, pattern recognition, and control systems. 5.2 Fuzzy Measures Definition A fuzzy measure (also called a non-additive measure or capacity) is a set function μ: 2^X → [0, 1] , where X is a finite set, satisfying: Boundary conditions : μ(∅) = 0 μ(X) = 1 Monotonicity : If A ⊆ B , then μ(A) ≤ μ(B) Unlike classical measures, fuzzy measures are not necessarily additive , meaning: Types of Fuzzy Measures Possibility Measure : Based on the degree of possibility; μ(A) = max{π(x) | x ∈ A} Necessity Measure : Dual to possibility; μ(A) = 1 − μ(Aᶜ) Sugeno λ-...